提到十二平均律,估计很多同学可能都会表示:这还不简单吗,不就是钢琴上一个组的十二个音嘛,七个白键加上五个黑键就构成十二平均律了。

这话说得虽然不是很严谨,但似乎也没什么太大的毛病。只是,你知道这十二个音是怎样定下来的吗?
1
八度的发现
十二平均律,也叫十二等程律,是目前世界范围内通用的把一个八度内的十二个音全部分成半音音程的律制。我们现在见到的绝大多数乐器,包括钢琴、吉他、小提琴等都是用这个律制来定音的。 这个现如今被普遍运用,看似很寻常的一个律制,其实却有着一段非常崎岖的身世。

两千五百多年前,在西方文化的源头古希腊诞生了一名杰出的数学家,他就是大名鼎鼎的毕达哥拉斯。毕达哥拉斯创立了毕达哥拉斯学派,致力于用数学解释自然界的一切难题。
在音乐上,毕达哥拉斯发现了“八度”的这样一个在当时看来很神奇的概念。即一个声音在将其频率提升至其二倍的时候,会产生一个另一个版本的该声音,两者几乎完全协和。
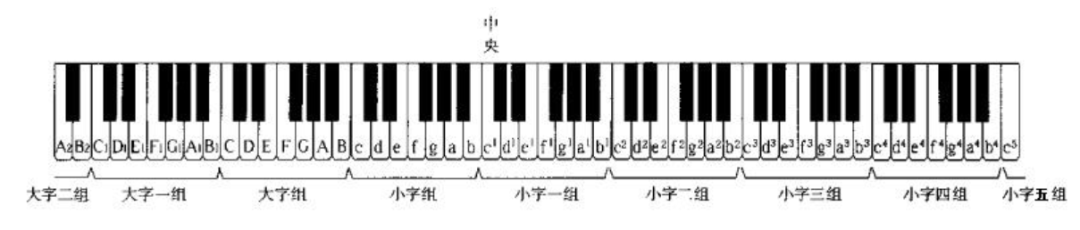
这个放在钢琴上来描述的话,就是像相邻组别的的C音之间这样的关系了。其实,在钢琴上,只要是相邻组别的同名音,较高的音比上较低的音,二者之间的频率都是2:1的关系。
2
基音无法还原
发现八度之后,这个痴迷于数学比例的男人又致力于寻找八度关系之外的音。于是,他又继续尝试了3:2的这个频率比例,然后便发现了一个新的音。
巧合的是,这个音与原本的音放在一起听也比较协和。这个音就是他发现的“纯五度”音。这个新的发现加深了他对自己关于音律理论认识的自信,认为用简单的整数比便可以求得最符合一般规律的音。

很自然地,他又开始把这个“纯五度”音再乘上3/2,得到了与基本音的频率成9/4的一个音。但,9/4已经比二要大了,所以,他再把9/4除以二,得到了与基本音的频率成9/8的一个音,即“大二度”音。依此类推,继续运用3:2和2:1的比例,就可以得到一个八度内的十二个音。
但是,就在最后一次算到第十二个音的时候,尴尬的事情发生了。最后这一个音于基音的倍数是531441/262144,很接近2,但是就是不是2,也就不是之前定下的那个高八度的音了。
按理说,如果最后一个音的倍数如果是2的话,就可以证明毕达哥拉斯的理论是完美的了,但是现实却不如人意。
虽然这两个数字很接近,在实际演奏当中,这个新的音是听起来不太舒服和协和的。这也导致后来的作曲家在写作品的时候会刻意地避开某些涉及到这类音的和弦。
3
新的律制的探索
过了一段时间,一些人开始觉得毕达哥拉斯这套理论不行,就自创了一套以他们所谓的“大三度”的5:4的比例为标准来制定的律制。但,这个律制同样也存在和毕达哥拉斯那个律制类似的问题,即基音无法还原。
真正出现转机是在后来人们的数学计算水平得到明显提高的时候。既然要有一种能够回归到2这个比例的律制,那么用2除以1再开12次方不就行了?2开12次方,拿计算器可以算出来是1.0594630943593……

这个数字貌似古人不大可能算得出来,但就在我国的明朝,那个还没有计算器的时代,我国古代著名的音律学家朱载堉却用我国自主发明的算盘,把这个数字给算出来了。他的这一研究成果领先西方近半个世纪。
采用这个数字比例之后,一个八度内的十二个相邻音之间的频率比例就都是这个数字了。虽然五音于基音的频率比例不再是特别协和的3/2,但在这个体系之下,与之前的律制相比,十二个音里除了八度音之外的所有音的频率都发生了偏差。
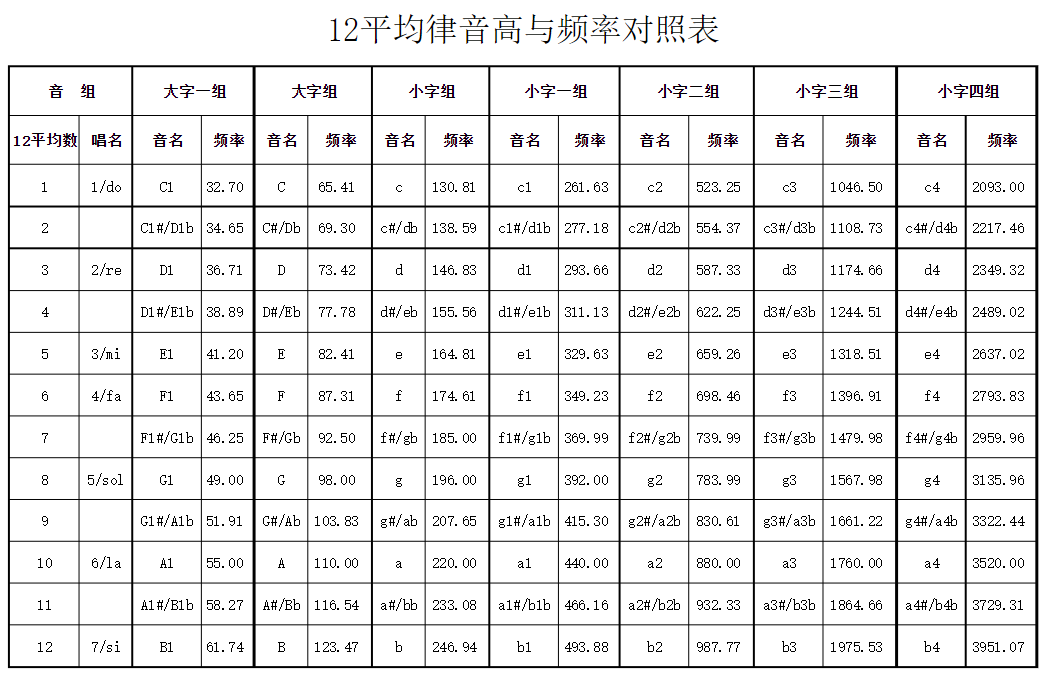
大家都不准,在听者听起来就是准的了。就像你和你的老师同学早上去上课的时候,大家都无一例外地迟到了,那可能,这节课就不算有人迟到了。
由此,十二平均律才算是正式地诞生了。
4
音乐与数学
说点题外话,自然界中好像真的没有什么东西是绝对完美的,音乐的不完美其实也只是其中的个例,像数学里那个经常用到的无理数e之类的就不提了。
但是,音乐确实跟数学有着千丝万缕的联系。数学好的人很大程度上都会喜欢甚至擅长音乐,比如说小提琴拉得很好的爱因斯坦,钢琴弹得很好的钱学森;相对的呢,学音乐的人也会喜欢甚至擅长数学,比如……(想不出来,有人可以补充一下吗……)

