本文作者：辰谙
相信学过一点基础乐理的同学们都知道，在音乐上，我们现如今最通用的律制就是十二平均律了。但是，这种律制并不是从一开始就存在的，它也并不是唯一的一种律制。
除了十二平均律之外，历史上还出现过一些别的律制，这些律制有的已经成为历史，有的则一直沿用至今。其中，最具代表性的莫过于五度相生律和纯律。
01
十二平均律
十二平均律又称“十二等程律”，是世界上通用的将一个八度分成十二个半音音程的律制，各相邻两律之间的频率之比完全一致。
我们知道，频率比为1:2的两个音是八度关系，而在一个八度中，一共有十二个音。要想使得各个相邻音之间的频率比值完全一致，那么最直接的方式就是算出2开12次方的结果。
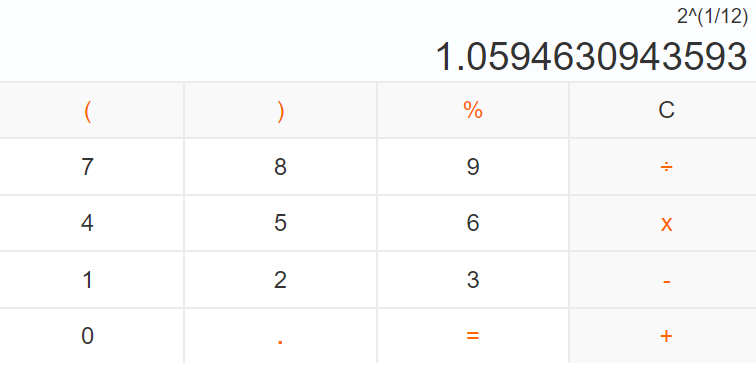
我们今天随便拿个计算器就可以得出2开12次方的结果，但是在计算器发明之前，人们想要得出这个结果却完全不是一件很容易的事。据记载，我国明代律学家朱载堉是历史上第一个算出2开12次方的结果的人。
在用这个数值计算出的结果中，纯五度音程的两个音的频率比（即1/2的7/12次方）约为0.6674，与我们接下来要讲的五度相生律的2/3，约为0.6667，非常接近。
02
五度相生律
五度相生律理论的诞生可以追溯到古希腊大数学家毕达哥拉斯对弦的音律的探索。
他根据弦的长度，以1:2为完全八度的比值，以2:3为完全五度的比值，把当时所用的音程都计算了出来。
五度相生律要求以某一个音为基音，然后将频率比为3：2的纯五度音程作为生律要素，分别向基音的上下两个方向同时生音。向上五次、向下六次或者向上六次、向下五次即可得到十二律。
比如说，假设以C为基音，按照五度相生法连续向上五次可得到G、D、A、E、B：
连续向下六次可得到F、Bb、Eb、Ab、Db、Gb：
以基音频率为1，八度音的频率为2，在五度相生律下可以得到一个八度内各音的频率如下：
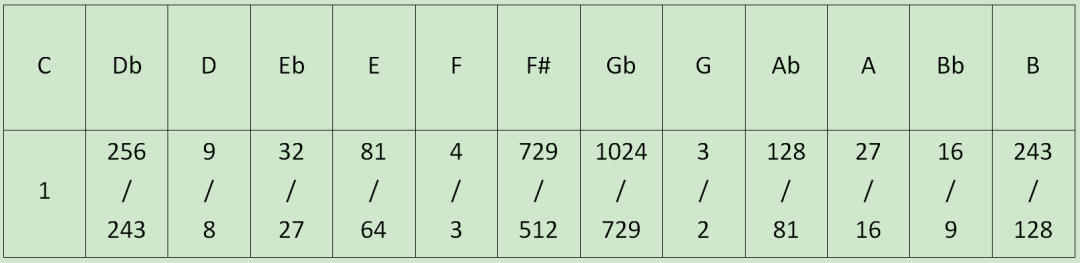
值得注意的是，在五度相生律的律制下，F#和Gb是两个不同的音，尽管它们之间的差别比较小。
03
纯律
纯律其实和五度相生律有着非常多的相似之处，事实上二者也有着一定的历史继承的关系。二者最大的不同之处就在于对基音与其大三度音程的处理上。 前面我们提到了，在五度相生律中，最重要的两个比例便是1:2和2:3，其所有律的生成都是靠这两个比例完成的。但是，相比五度相生律，纯律中又添加了一个新的比例关系，即4:5，应用于基音与其大三度音程的关系上。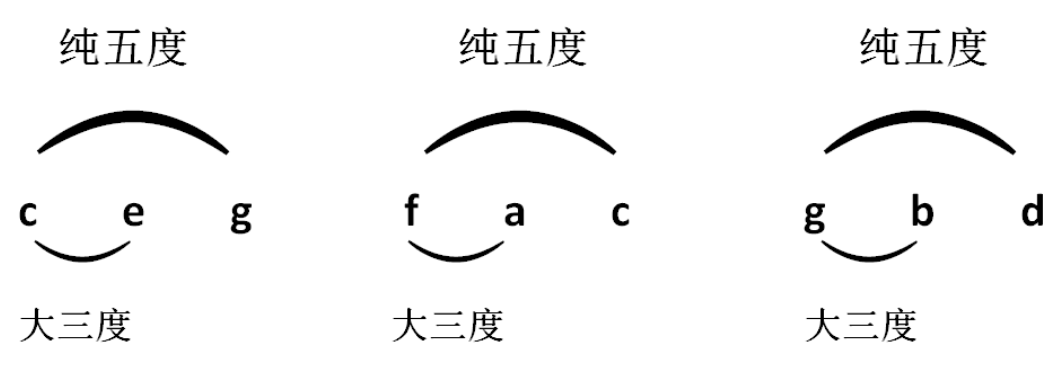 
按照五度相生律的计算方式，我们可以得到基音与其大三度音的比例关系为64:81，并不是简单的整数比。而纯律相对于五度相生律做出的改变就在于把这个比例直接改成了简单的整数比4:5。 在纯律的理论中，大七度为纯五度加大三度，小三度为纯五度减去大三度。由于纯律音阶中各音对主音的音程关系与纯音程完全相符且其音响非常协和，故称“纯律”。 
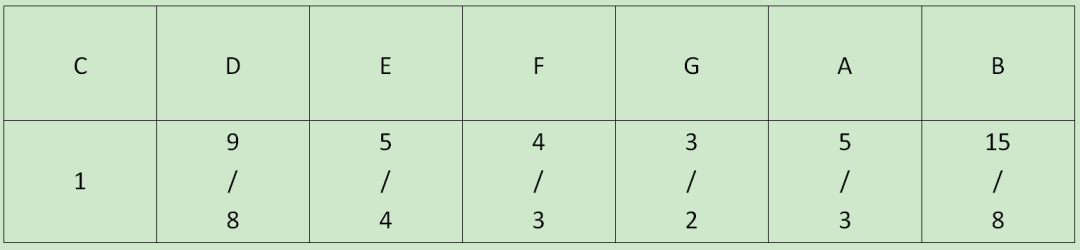在纯律中，EF、BC之间的半音比其他两种律制的半音要大。而全音的情况则有两种，即CD、FG、AB为大全音，和五度相生律中的全音相等，比十二平均律中的全音大；DE、GA为小全音，比其他两种律制的全音都小。 我国古代虽然没有出现过关于纯律的理论，但在古琴第3、6、8、11四个徽，依次当弦长比为1/5、2/5、3/5、4/5的四处，其比值的分母均为5，这一点是纯律所独有的特征。而据相关考证，更是可以推断我国在战国时期就已经应用了纯律。
