尺八这种乐器与西方许多乐器有著根本上的差异,泛音与噪音是其中一项备受争议的项目,很多人使用频谱分析仪分析泛音,倍频...,也得到许多很有趣的资讯,常听到"这支尺八声音比较好""这支尺八筒音音色比较耐听,响度大....,这些都对,也都是有原因的,从频谱上可以略窥一二.
泛音的多寡,强弱对尺八音色有非常大的影响,泛音对声音传播的远近也有决定性的影响,以下文章中节录出的说法对声音组成的要素提供相当程度的理论根基,懂得善用频谱,也能让您对您手上的尺八有更进一步的了解,个人认为,製管师应该善用这项利器为自己的尺八作更深入的验证.耳朵虽是最后把关的唯一选择,但制作过程中,频谱也是一项重要参考依据. 用科学的方法验证乐器的优劣未必准确,但不好的乐音也真的很难看到漂亮的频谱分佈图.
"意大利美声学的观点,就是将基音到第16个泛音的强度在坐标上连成一条直线,这条直线就被称为最佳美声线。那麽,哪个音色的频率特性曲线越接近这条直线,哪个音色的低、中、高频泛音的比例也最为均衡,其音色的艺术表现力也最为尚佳。
"
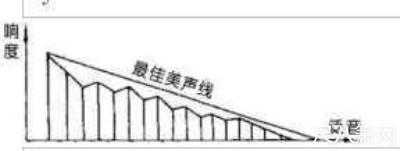
"钢琴的最低音频率是27.5Hz,最高音频率是4186Hz,而钢琴有十几个泛音,它的高频可达10kHx~20kHz,一般可测到16个泛音或24个泛音。这些泛音可分为低频泛音、中频泛音和高频泛音,。如果低频泛音的幅度较强,音色就表现得混厚;中频泛音的幅度比较强,音色就表现得圆润、自然、和谐;高频泛音的幅度比较强,音色就表现得明亮、清透、解析力强。"
有人说"噪音是尺八吹奏的一部分",但尺八气息声对吹奏长笛的人几乎是无法接受的杂音,但尺八吹奏中却常见到,以下这篇文章对这部分的问题提供了一部分的解答,值得好好读读. 因为文件为pdf档案,图型转换比较麻烦,建议点阅原始网页阅读.
带有杂质的乐音──听觉模型及「泛音-噪音比」
Copyright 作者 : 蔡振家(国立台湾大学音乐学研究所助理教授)
http://crimson.ee.ncku.edu.tw/wordpress/wp-content/uploads/2009/06/impure_m_6.pdf
摘要
在西方古典音乐里面,带有杂质的音色似乎不如纯淨的乐音来得悦耳,因此音乐家
通常会刻意避免产生这类音色,但在某些音乐文化中,嘈杂不纯的音色却是音乐风格中
不可分割的一环。本文从音景分析(auditory scene analysis)理论来建立嘈杂音色的听觉模
型,并以频谱图与「泛音-噪音比」(harmonic-to-noise ratio)来分析器乐与声乐里的各种嘈
杂音色。
关键字
音色、泛音-噪音比、音景分析、吼音、尺八、电吉他、京胡
Impure musical sounds: auditory model and harmonic-to-noise ratio
Abstract: In western classical music, the impure timbre is more unpleasant than the timbre
without any impurity. Therefore, musicians usually intentionally avoid the production of the
former timbre. In other musical cultures, however, the impure timbre is an integral part of
musical styles. The present paper proposes an auditory model for the impure timbre on the
theoretical basis of auditory scene analysis. Examples of the impure timbre in instrumental and vocal music are analyzed with spectrograms and harmonic-to-noise ratios.
Keywords: Timbre, harmonic-to-noise ratio, auditory scene analysis, growl voice, shakuhachi,
electric guitar, jinghu
《关渡音乐学刊》10:113-125, 2009
2
一、前言:noise control 或well-controlled noise 音色在乐曲的进行中经常佔有举足轻重的地位,然而,它却是一个难以分析的音乐
面向。相较于音高与音量,音色的量化分析无法由一个参数来完整描述,1而必须用到频
谱分析(spectral analysis)、包络分析(envelope analysis)......等工具,与此相关的研究方法已
经跨出了人文、艺术学科,而属于音乐声学(music acoustics)的范畴。音乐声学是一门探
讨乐音的产生(production)、传播(transmission)、知觉(perception)的学科。由于音乐与文化、
历史密不可分,音乐声学与声学的其他次领域相较之下,实具有不易捉摸、浪漫缥缈的
特质。举例而言,声学中的次领域之一:噪音控制(noise control),旨在减低噪音与不必要
的振动,目标清楚,但音乐声学家在追求性能更佳的乐器时,却常常连自己也说不清楚:
什麽样的音色是好听的、什麽样的振动才是演奏者想要的?虽然噪音总是带给听众不舒
服的感觉,但音乐家并没有完全抹除这些噪音,相反的,有些音乐家特别擅长使用嘈杂
不纯的音色,因此,音乐声学里面的noise control 似乎也有著另一层积极的意义:
well-controlled noise,意即「随心所欲地控制噪音的产生、并在乐曲中巧妙使用」。
本文所要探讨的,便是一些带有杂质的沙棱音色,以及它们在音乐中的运用。当乐
器或歌手发出一个稳定、纯淨的音时,频谱上只会出现一系列的泛音,其频率为音高f
的整数倍;当声音变得嘈杂不纯时,相邻泛音之间会出现杂质。频谱分析可以进一步区
分这些杂质:对称出现在泛音谱线两侧的称为旁带(sideband)、在相邻泛音之间等距分佈
者(频率为f/m 的整数倍,m = 2, 3, 4...)称为次泛音(subharmonic)、在相邻泛音之间连续
分佈的称为噪音。本文除了提出此类音色的听觉模型之外,亦将举出各种乐器与音乐文
化中的实例,探讨乐音杂质的产生机制(production mechanism)与量化分析的方法。本文将
指出,原本用以分析语音之「泛音-噪音比」(harmonic-to-noise ratio)的计算软体,也适用
于分析音乐,对于有志于研究音色的音乐工作者而言,是个便于使用的研究工具。
二、嘈杂音色的听觉模型
嘈杂度(roughness)泛指声音中不悦耳、不乾淨的音质,十九世纪的科学家Hermann von
Helmholtz (1885/1954)把嘈杂度归因于频率相近的频谱成份之间所产生的「拍」(beating)。
1960 年代之后,嘈杂度理论进一步与临界频带(critical band)的观念相结合。临界频带的听
觉模型告诉我们,耳蜗对声波所作的频谱分析,是将听觉范围(从20 Hz 至22000 Hz)
分割为二十几个频道(channel),每个频道就是一个临界频带,只有当两个音落在同一个临
界频带中才会产生嘈杂音质,该临界频带中所接收的声音讯息是忽强忽弱的「拍」(Plomp
and Levelt 1965)。
一个音高为100 Hz 的低音,若其音质明亮,会有丰富的高频泛音,根据临界频带的
听觉模型,超过2000 Hz 的泛音将造成嘈杂的音质,因为这些泛音之间的频率差只有100
1 例如频率可以完整描述音高、声压(sound pressure level)可以完整描述音量。
《关渡音乐学刊》10:113-125, 2009
3
Hz。有趣的是,音质明亮的低音(例如男、中低音的歌声)并不会给人特别嘈杂的感觉,
我们也不会在这类乐音中听到「拍」的现象,由此可见传统嘈杂度听觉模型的缺失。笔
者曾经根据de Cheveigné (1997)所提出的泛音干扰消去(harmonic interference cancellation)
模型,提出一个对于传统嘈杂度听觉模型的修正:当一个音的音高f 清晰可闻时,频率为
nf 的泛音会被整合在一起(n = 1, 2, 3, ...),并不会彼此干扰而造成嘈杂音质(Tsai 2004)。
週期性的声波在自然界十分普遍,虽然频谱分析可以发现它们包含许多泛音,但我
们却总是听不到个别的泛音,听觉系统似乎是把所有的泛音整合为同一个音。2将传入耳
中的声音予以分解为许多元素、再将可能来自于同一声源的元素整合在一起,这样的机
制称为音景分析(auditory scene analysis)。整合声音元素的规则(grouping rule)包括了:(1)
频率比呈整数关系的泛音倾向于被整合在一起(harmonicity),(2)同时出现的声音元素倾向
于被整合在一起(common onset),(3)一齐变化的声音元素倾向于被整合在一起(common
modulation)……等(Bregman 1990)。本文所探讨的嘈杂不纯音色,主要都是源自于泛音之
间的频谱成份,包括次泛音、旁带、噪音等,由于这些频谱成份无法被上述的第一条规
则harmonicity 所整合,因此会被听觉系统判断为杂质。本节所提出的听觉模型,将以含
有次泛音的中国笛笛音为例,逐步说明音景分析的原理。
图一为嘈杂音色的听觉模型示意图。声波传入听觉系统之后,由快速傅立叶转换(fast
Fourier transform; FFT)之类的运算得到此音的频谱图(图一a),此笛音的频谱特色是次泛
音分佈于两个相邻泛音的正中央。而在另一方面,声波经由autocorrelation 之类的运算可
得到其週期T (Licklider 1951, Meddis and O’Mard 1997),以及音高f = 1/T。下一步骤为最
重要的筛选(sifting),根据f 所建立的泛音范本(harmonic template)可以视为有许多洞的筛
子,各个洞皆位于f 的整数倍,因此,泛音可以通过此一筛子,次泛音或噪音则无法通过
此一筛子。频谱成份经过筛选之后,通过筛子的泛音(图一b)将被整合在一起,是此音
的纯淨成份(pure part);未通过筛子的次泛音与噪音,则被视为此音的杂质。
在这个听觉模型中,特别值得注意的是提取音高(pitch extraction)此步骤所扮演的关
键角色。若此笛音的音高是f/2,则原本的次泛音便可通过泛音范本的筛选,被整合为此
音的纯淨成份。然而,此笛音的次泛音在低频范围(< 2 kHz)十分微弱,容易被相邻的泛音
所遮蔽(mask),因此由低频的频谱成份来提取音高时,次泛音可以忽略,得到的音高不是
f/2 而是f。虽然次泛音在高频范围(> 5 kHz)的强度已与相邻泛音不相上下,能够影响音
色,然而它们的频率太高,故无法影响音高的知觉。
2 当某个泛音特别突出时,它可以被独立听到,于是造成新的音高,这种情形仅会发生在少数
乐器上面,例如:口簧琴(Jew’s harp)、弓琴(mouth bow)......等,此外还有泛音唱法(overtone singing)所产生的歌声。
《关渡音乐学刊》10:113-125, 2009
4
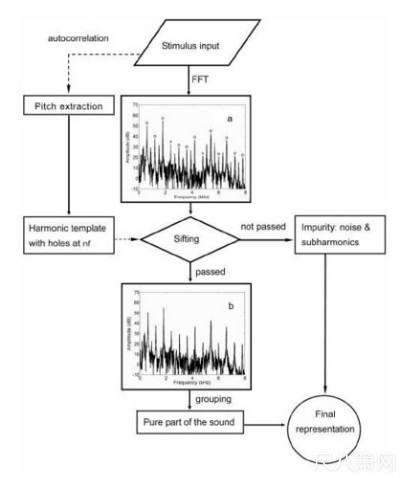
图一:嘈杂音色的听觉模型示意图,详见本文的说明。(a)含有次泛音的笛音频谱图,横
轴为频率,纵轴为分贝,标上“。”记号的是频率为nf 的泛音谱线,在这些谱线的之间
可以观察到次泛音谱线。此笛音取自俞逊发演奏的CD 专辑《寒江残雪》(琴园出版社),
第八曲《妆台秋思》的3 分20 秒处。(b)含有次泛音的笛音经过泛音范本筛选之后,次泛
音会被去掉,此为近似的频谱图。
《关渡音乐学刊》10:113-125, 2009
5
三、器乐与声乐中的嘈杂音色
本节举出一些带有杂质的乐音例子,并简述其发声原理。由于上节的听觉模型强调
了声音中的纯淨成份与杂质,因此,本节亦将尝试以「泛音-噪音比」(以下简称HNR)
作为量化分析的指标,这个指标的定义为「泛音的能量总和除以其他频谱能量的总和」,
单位通常为分贝(decibel)。本研究中的计算方法,是使用语音分析软体Praat 5.0.23 (Institute
of Phonetics Sciences of the University of Amsterdam. http://www.praat.org)中的short term
HNR analysis(在该软体中被归类为harmonicity 方面的处理),其运算基础为autocorrelation
(Boersma 1993)。以语音分析软体来处理乐音,其适用性如何?「泛音-噪音比」是否为乐
音杂质的良好指标?这都是以下音乐实例中所要探讨的议题。
(一)京胡的开花音
京胡演奏技法中的开花音又称虚实音、虎音、炸音、人工噪音......等,在京剧老生、
青衣、淨角、老旦唱腔的伴奏中具有渲染情绪的作用。其奏法是让左手手指放鬆、轻触
琴弦(称为「泛按」),同时右手用力拉出音头,如此便能奏出强劲的噪音。由于左手手
指与琴弦之间仅有微小的距离,故琴弦振动时会不断碰撞左手手指,在琴弦上行进的波
也会受到不规则的干扰,因此能产生丰富的高频噪音(蔡振家2008)。

图二:京胡开花音的spectrogram(图下方)与HNR(图上方)。此段音乐取自光碟《京
胡古今名段》(中国青年出版社),由京胡名家燕守平讲解并演奏。
《关渡音乐学刊》10:113-125, 2009
6
演奏开花音时,左手可以用一根指头泛按琴弦,待右手拉弓到一半时,左手指头再
按实,右手回弓、左手揉弦,此一奏法又称为虚实音,意即左手按弦「先虚后实」。如此
拉推弓连续数次,可在同音反覆中做出音色变化,图二a 显示了这种虚实音的
spectrogram,此音的特色是噪音与泛音列交替出现:当左手食指紧按琴弦时,频谱上可看
到一系列的泛音;而当食指稍微离开琴弦产生开花音时,频谱上的泛音变得模糊,取而
代之的是散成一片的噪音。HNR 随时间变化的情形如图二a 上方曲线所示,当左手食指
紧按琴弦时,HNR 大致高于15 dB,而当左手食指泛按琴弦时,HNR 则骤降至10 dB 以
下。
图二b 为一段旋律在京胡上连续演奏三次的spectrogram,京胡演奏家讲究的是:第
一个音要略带杂质(称为「小开花」),而杂质的多寡可由左手手指轻触琴弦的方式来微
调。图二b 的三次演奏中,第一次演奏的开花音含有最多的噪音,第二次演奏的开花音
最纯淨,第三次演奏的开花音则有几个次泛音出现在频率为5f/2、7f/2、9f/2 之处。这三
次演奏的开花音HNR 也随著杂质的多寡而规律变化,但变化幅度不大。
(二)膜笛的幽咽音色
中国笛能发出类似沙哑嗓音的幽咽音色,这类声音的特徵是含有次泛音,例如频率
为f/2、3f/2、5f/2、7f/2……等的音,其中f 为该音的音高。中国笛的笛音中存在次泛音的
现象,跟人声的情形有点类似,也就是次泛音会使音色变得嘈杂不纯,不过中国笛的物
理原理与人声毕竟相当不同,中国笛只在特定的音域才会产生次泛音。以C 调曲笛为例,
在吹奏第一个八度,也就是从G4(最低音)到F5 时,并不会有次泛音产生,在吹奏G5、
A6、B6、C6 等音时,则会出现次泛音。这样的笛音可以视为在该音中混入了一些低八度
音的成份,这些成份就是频率为(2n-1)f /2 的次泛音(n = 1, 2, 3, ...)。因此,具有次泛音的
音可视为「八度双音」(octave multiphonics),它也会发生在长笛初学者的演奏之中,在西
方古典音乐中通常会刻意避免这类不乾淨的音色。反之,贴有笛膜的中国笛,则因为笛
膜的非线性特质而具有更强的高频次泛音(蔡振家2005),这也就成了中国笛曲的声响特
点之一,特别是低音笛。
图一a 与图一b 所示的两个的笛音,去掉次泛音的结果是让HNR 从19.3 dB 上升到
了19.8 dB,可见HNR 的值对于频率为(2n-1)f/2 的次泛音之存在与否并不敏感,这个现象
与图二b 的京胡开花音之HNR 值变化甚微大致类似。
(三)尺八的气音
日本的尺八源于中国唐宋时期的尺八,它与近代中国的洞箫虽然系出同源,但在演
奏风格上却有很大的差异,其中最明显的差异可能就是:日本尺八非常强调口风的变化,
并以此产生紊流噪音(turbulence noise) ,尺八的演奏者以「ムラ息」来指称这种可以发出
丰富噪音的技巧,意即「不均匀的气息」。这种演奏技巧一般是让嘴唇靠近吹孔、吹出强
劲的气流,乐谱上通常记为、、等,3其音色可以让人联想到自
3 参考网页http://www.shakuhachichambermusic.net/pages/notatingwm.html,浏览日期
2008/12/16。
《关渡音乐学刊》10:113-125, 2009
7
然界的风声。由于近年日本电影、卡通中会以尺八来陪衬武士、忍者的打斗,「ムラ息」
也似乎便成为代表「肃杀之气」的声音。
4
图三:尺八的「ムラ息」,乐音的spectrogram(图下方)与HNR(图上方)。此音取自美
籍音乐家Elizabeth Reian Bennett 的尺八CD 专辑Song of the True Hand,第七曲《遍路》
的2 分55 秒至3 分0 秒。
除了传达杀气之外,尺八的「ムラ息」也可以用来象徵肉体与精神上的力量,例如
在枡屋正邦所谱作的尺八独奏曲《遍路》(Henro)裡面,「ムラ息」便常用来表现朝圣者在
艰难旅途中的奋斗力量(Keister 2008)。图三分析了《遍路》曲中的一个「ムラ息」,从频
谱图中可以看到,此音中间有显著的宽频噪音,而该处的HNR 也降到了最低点。
(四)萨克斯风与铜管乐器的吼音
在爵士乐与摇滚乐里面,萨克斯风、小号、长号都可以使用吼音(growling)的技巧来
增加乐音的杂质,方法是在吹奏的同时由喉部唱出声音。当声带与嘴唇同时振动时,两
者有可能同步化(synchronization)而以呈简单整数比的频率振动(Gibiat and Castellengo
2000),或是以torus 为吸子而产生旁带,或是以混吨式(chaotic)的振动行为产生宽频噪音。
以上这三种可能性的发生,取决于声带与簧片(或嘴唇)的弹性、气流大小、共鸣管……
等因素,所造成的声音杂质也有多种变化。图四所示的spectrogram 是在小号上运用吼音
技巧的例子,可以发现,此音开头较为纯淨的音色,其HNR 大致高于30 dB,而在杂质
4 十六世纪日本出现普化宗,尺八成了普化宗虚无僧的法器,到了德川幕府时代,政府利用普
化宗作为「勇士浪人之隐家,武人修行之宗门」,武士们也连带吸收了普化宗的尺八艺术,此后,尺八便与武士结下了不解之缘。
《关渡音乐学刊》10:113-125, 2009
8
较明显的3.4 秒至6 秒之间,HNR 则低于10 dB。
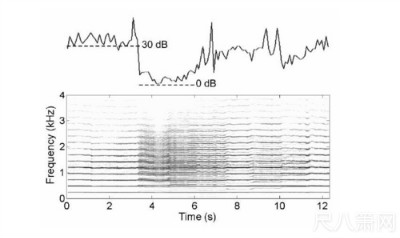
图四:小号的吼音技巧,乐音的spectrogram(图下方)与HNR(图上方)。此音由赵彦
婷示范演奏。
(五)歌声中的杂质
在多采多姿的歌声中,也有一些带有杂质的沙棱音色。撇开喉部组织病变的情形不
谈,专业歌手的沙棱音色常常源于声门上结构(supraglottic structures)的振动。嗓音的发生
是由于肺部呼出空气、声带靠拢,气流通过声带间的狭缝(称为声门)导致声带振动。
在喉部组织中,除了声带可以振动之外,声带上方的一些声门上结构偶尔也会振动,在
发声时佔有一席之地。声门上结构包括了一对假声带(false vocal fold)与杓状会厌软骨皱褶
(aryepiglottic fold)等。从生物演化的角度来看,声门与声门上结构原本可能都是阻挡食物
或水进入气管的关卡,但它们刚好也可以用来振动发声,其中声带进一步演化为极有效
率的发声器官,在上皮与韧带之间有个富含液体的空间,称为Reinke’s space,是声带中
振动最剧烈的区域,其丰富的含水量让声带更柔软、振动更为容易。声带可以在骨骼肌
的牵引之下改变张力、形状与振动频率,发出不同的音高。声门上结构在一般的发声状
态中并不会振动,但在咳嗽或吼叫等情形,它们会向中央靠拢,当气流通过其间的狭缝
时,便会引起表面黏膜的振动。不过声门上结构里面没有骨骼肌,因此无法随心所欲地
改变它的弹性。
在发出吼叫式的嗓音时,声带与声门上结构可以同时振动,但两者的振动频率却不
一样,这种情形与萨克斯风、铜管乐器的吼音类似,也会产生次泛音、旁带、噪音。在
爵士乐坛中,有不少歌手以沙质嗓音唱出韵味醇厚的歌曲,而摇滚音乐、重金属音乐的
表现益趋激烈,医学研究证实,摇滚歌手的嘶吼常伴随著声门上结构的振动(Borch et al.
《关渡音乐学刊》10:113-125, 2009
9
2004)。除了摇滚歌手之外,科学家也曾研究过俄罗斯传统歌乐(Mazo et al. 1995)、朝鲜传
统民间歌乐(Lee et al. 1998)裡面的歌声杂质。
在中国戏曲里面,京剧的架子花脸经常会发出炸音,成为其唱腔的特色之一(蔡振
家2005)。图五所示的例子中,架子花脸的唱腔由纯淨的音色转为炸音,声波的包络可
以看到调幅(amplitude modulation)的现象(1.65 秒附近),调幅频率约为89 Hz,此即声门
上构造的振动频率,而声带的振动频率约为445 Hz。纯淨歌声与炸音的HNR 值分别为
19.8 dB 与3.6 dB,可见HNR 确实能反映歌声中杂质的多寡。
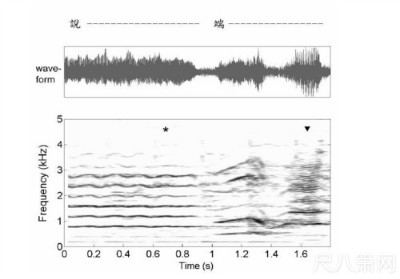
图五:京剧《李逵探母》唱段中的炸音。架子花脸由杨赤饰演,唱词为「老娘不必珠泪
降,细听孩儿说端详」,此例中仅分析「说端」二字。计算结果显示:纯淨歌声(*)与
炸音(▼)的HNR 值分别为19.8 dB 与3.6 dB。
(六)电吉他的破音
破音是许多人对于电吉他的第一印象,从电吉他的发展史来看,破音的起源可能是
吉他手Paul Burlison 于1956 年使用损坏的扩大机所得到的意外效果,后来也有吉他手故
意把喇叭单体刺穿以扭曲音色(Walser 1993:42)。有鉴于电吉他演奏者对于破音的需求,製
造音箱的公司也在产品中发展「以信号过度增益造成失真」(clipping)的效果,如今,电吉
他的效果器可以做出distortion/overdrive 等破音。
同时弹奏电吉他的数根弦,能够凸显效果器所产生的破音音色,因为原本讯号中的
《关渡音乐学刊》10:113-125, 2009
10
频谱成份在非线性扭曲之下,可产生许多组合音(combination tone),其频率为原本频谱成
份的整线性组合(integer linear combination)。5可惜的是,这类的乐音虽然富含杂质,但却
不适合进行HNR 分析,因为HNR 分析基本上只适用于单音音乐。电吉他中有一种「同
音推弦」的技巧,适合进行HNR 分析,因为这种音是同时在两根弦上弹奏音高接近的两
个音(通常差一个全音),然后左手手指将音较低的弦向外推,让两根弦的音高渐趋吻合。
这种音的开头富含杂质,其为「拍」加上破音效果的产物,而当两个音逐渐接近时,杂
质便会越来越少。图六显示了电吉他「同音推弦」的频谱图与HNR,图中可以观察到HNR
随著频谱杂质的递减而递增,从原本的0 dB 增加到约30 dB。这种富含杂质的音头可以
製造音乐的张力,而杂质的逐渐消失,则可以导致张力的解决,因此,「同音推弦」似乎
可以视为一种「音色的终止式」。
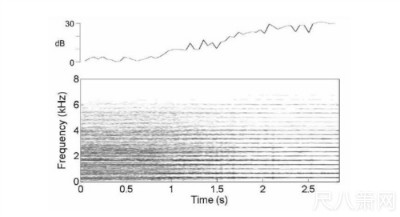
图六:电吉他的扭曲效果,乐音的频谱图(下方)与HNR(上方)。此音取自Troy Stetina
所著Metal Lead Guitar Vol.1 所附的CD。
四、结论
在西方古典音乐里面,带有杂质的音色似乎不如纯淨的乐音来得悦耳,因此音乐家
通常会刻意避免产生这类音色;但在中国戏曲、爵士乐、摇滚乐等音乐文化中,嘈杂不
纯的音色却是音乐风格中的「蒜酪之味」,虽为点缀性质,在许多乐曲中都少不了它的「调
味」。本文根据音景分析的理论指出,这些乐音的杂质未能通过由音高f 所建立的泛音范
本筛检,所以才被当作杂质。
乐音中杂质的多寡,可用HNR 值来估计。在各种杂质裡面,噪音与旁带较能影响
5 例如若原本有两个频谱成份之频率为f1 与f2,经过非线性扭曲之后,会产生频率为∣mf1 + nf2
∣的频谱成份,其中m 与n 为整数。
《关渡音乐学刊》10:113-125, 2009
11
HNR,反之,HNR 的值对于频率为(2n-1)f/2 的次泛音之存在与否并不敏感。一般而言,
纯淨乐音的HNR 都大于15 dB,而泛音丰富的铜管乐器声,其HNR 甚至可以高达30 dB。
带有杂质的乐音,其HNR 通常低于15 dB,而当HNR 低于5 dB 时,音色听起来便十分
沙棱。此结果与一项针对犬吠声的研究大致吻合,该研究发现,泛音特别丰富的嘹亮犬
吠声,HNR 大于20 dB;而声带病变的犬隻,其吠声富含杂质,HNR 低于10 dB (Riede et
al. 2001)。
音乐家在演奏(演唱)时添加杂质的手法,背后有各种不同物理机制,端视所使用
的乐器而定。簧片乐器、唇振乐器与人声通常是让两个非线性振盪系统产生藕合,擦絃
乐器可以运用手指轻触琴弦的技巧,而电吉他则是在电子讯号处理中製造失真,产生扭
曲效果。从传统音乐到电子时代,乐音的杂质即使不一定直接由演奏技法产生,但在演
奏时「妥善控制噪音、予以巧妙运用」的原则,并没有基本上的改变,由此可见杂质在
乐音之中的重要地位。
参考文献
Boersma, P. (1993). Accurate short-term analysis of the fundamental frequency and the
harmonics-to-noise ratio of a sampled sound. Proceedings of the IFA, 17: 97-110.
Borch, D. Z., Sundberg, J., Lindestad, P. A., and Thalén, M. (2004). Vocal fold vibration and
voice source aperiodicity in 'dist' tones: a study of a timbral ornament in rock singing.
Logopedics, Phoniatrics, Vocology, 29(4): 147-153.
Bregman, A. S. (1990). Auditory Scene Analysis. Cambridge, Massachusetts: MIT Press.
de Cheveigné, A. (1997). Concurrent vowel identification. III. A neural model of harmonic
interference cancellation. Journal of Acoustical Society America, 101: 2857-2865.
Gibiat, V., and Castellengo, M. (2000). Period doubling occurrences in wind instruments
musical performance. Acustica, 86: 746-754.
von Helmholtz, H. L. F. (1885). On the Sensations of Tone as the Physiological Basis for the
Theory of Music. 2nd ed. trans. A. J. Ellis, from German 4th ed. (1885), Reprinted,
Dover, New York (1954).
Keister, J. (2008). Song of the True Hand (Audio Recording Reviews). Asian Music, 39(2):
194-197.
Lee, M. H., Lee, J. N., and Soh, K. S. (1998). Chaos in segments from Korean traditional
singing and Western singing. Journal of Acoustical Society America, 103(2):
1175-1182.
Licklider, J. C. R. (1951). A duplex theory of pitch perception. Experientia, 7(4): 128-134.
Mazo, M., Ericson, D., and Harvery, T. (1995). Emotion and expression: temporal data on voice
quality in Russian lament. In: Vocal Fold Physiology: Voice Quality Control, ed. O.
Fujimura, and M. Hirano, San Diego: Singular, pp. 173-187.
《关渡音乐学刊》10:113-125, 2009
12
Meddis, R., and O’Mard, L. (1997). A unitary model of pitch perception. Journal of the
Acoustical Society of America, 102: 1811-1820.
Plomp, R., and Levelt, W. (1965). Tonal consonance and critical bandwidth. Journal of the
Acoustical Society of America, 38: 548-560.
Riede, T., Herzel, H., Hammerschmidt, K., Brunnberg, L., and Tembrock, G. (2001). The
harmonic-to-noise ratio applied to dog barks. Journal of Acoustical Society America,
110(4): 2191-2197.
Tsai, C. G. (2004). Auditory grouping in the perception of roughness induced by subharmonics:
empirical findings and a qualitative model. Proceedings of the International
Symposium on Musical Acoustics (March 31-April 3, Nara, Japan), pp. 257-260.
Walser, R. (1993). Running with the Devil: Power, Gender and Madness in Heavy Metal Music.
Hanover, NH: University Press of New England.
蔡振家(2005)〈表演者的混吨嗓音-吼音的跨领域探讨〉。《戏剧学刊》,第2 期,页39-62。
蔡振家,Auhagen, W. (2005)〈中国笛的音准、音域与音色:笛膜的Duffing 振子模型〉
(http://homepage.ntu.edu.tw/~gim/gia/pub/dizi6.pdf)。传统乐器学术研讨会,2005
年9 月10-11 日,台北,台湾。
蔡振家(2008)〈具有非线性边界条件的琴弦振动:京胡“开花音”的声学研究〉。《黄锺
─武汉音乐学院学报》2008 年4 期,页168-173。
摘自台湾山城(王锦德)老师部落格

